4.8 两因素（析因设计）方差分析

最后更新：2021-10-25

【例】两种镇痛药物的3×3析因设计方差分析

观察A、B两种镇痛药物联合运用在产妇分娩时的镇痛效果。A药取3个剂量：1mg，2.5mg，3mg；B药取3个剂量：5μg，15μg ，30μg ，组合为9个处理组。

将27名产妇随机等分9组，记录分娩时联合用药的镇痛时间，结果如下表所示：

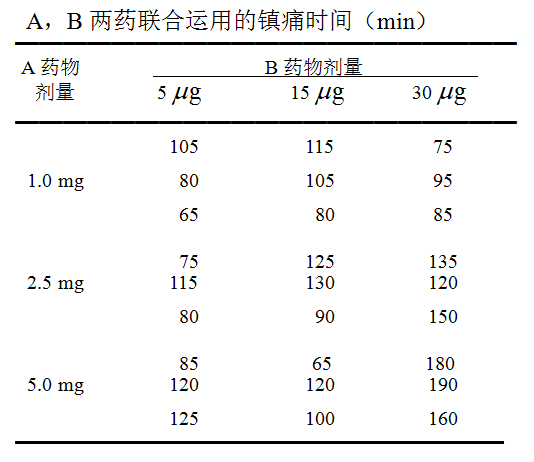
（注：数据引自《医学统计学》第3版，孙振球, 徐勇勇，人民卫生出版社 2010.08，P198:例11-2）

试分析A、B两药联合运用的镇痛效果。

---

==假定本研究的数据满足方差分析的一般条件==，即：

• 独立：不同个体（观察值）相互独立
• 正态：不同组别的观察值均服从正态分布
• 方差齐：不同组别的观察值方差齐（方差相等）

则可使用析因设计的方差分析方法，分析A药、B药不同剂量水平的镇痛效果差异，以及A药与B药的交互作用。

使用SPSS对该数据进行统计分析的具体过程如下：

1. 建立数据集

建立好的数据集，数据列表如下所示：

变量视图：

需设置3个变量：

变量A：A药的剂量，共3个水平，分别以1、2、3代表1.0mg、2.5mg、5.0mg（变量的value/label非必要）；

变量B：B药的剂量，共3个水平，分别以1、2、3代表5ug、15ug、30ug（变量的value/label非必要）；

变量T：镇痛时间

2. 方差分析操作

选择一般线性模型（General Linear Model）中的单变量（Univariate）分析方法：

变量的设置：

把处理因素全部放在固定效应因素列表中，即该一般线性模型为固定效应模型；本例为析因设计的方差分析，Model选项可以不作设置，实际使用的模型为默认的Full factorial（完全析因）模型，如下图：

本例的Full factorial模型，包含了A因素、B因素，以及A与B的交互项。

==如果（本例非必要）==点击上图中的Custom进行模型的自定义：

则模型中包含A、B与AB交互项时，就相当于选择了Full factorial模型；若模型中不包含AB交互项，则本例就变为随机区组设计的方差分析过程了。

变量与模型均设置好，点击【OK】按钮即可输出统计结果。

3. 结果解读

（SPSS 23 64位）输出的统计结果如下：

统计结果显示：

A药的不同水平（不同剂量组），差异有统计学意义（$F=8.47, P=0.03$）；

B药的不同水平（不同剂量组），差异有统计学意义（$F=9.05, P=0.02$）；

AB两药之间的交互作用有统计学意义（$F=5.073, P=0.06$）。

若想进一步了解A药、B药具体哪些剂量组之间存在差异，可进行方差分析的多重比较，参见4.4 完全随机设计的方差分析（单因素方差分析）实例。

通过作图的方法，可进一步了解AB两药的交互作用，操作如下：

输出的交互作用图如下：

根据镇痛时间的边际均值（Marginal Means）估计值可知，A药5.0mg与B药30μg联用时，镇痛时间最长。

© By StatX..