6.2 两个计量资料/等级资料的简单线性相关分析

最后更新：2024-10-12

相关分析，不强调变量之间是否存在因果关系，这是其与回归分析最大的区别；相关分析仅仅关心变量之间是否有共变的关系而无论有无因果关系，所以相关分析中的不同变量，地位是相同的。

对于服从（或近似服从）正态分布的两个变量，可进行简单线性相关(simple linear correlation)分析，以推断两个计量资料在数值上的线性共变关系，也称Pearson相关（Pearson Correlation）；若数据不服从正态分布，或有明显的离群值（Outliers），或者为等级资料，可使用Spearman相关分析（Spearman Correlation），也称Spearman秩相关分析。

相关具有方向性，若总体相关系数$\rho \gt 0$则称之为正相关，反之，$\rho \lt 0$称之为负相关。

前提条件：

两个变量进行相关分析，需满足的前提条件相对宽松，如上所述。

应用场景：

两个计量和/或等级资料，推断其数量上的共变关系。Pearson相关方法推断的是线性相关，Spearman相关方法推断的是秩相关。

【例】成年儿子与父母身高的相关关系

我们从 6.3 多个自变量的多重线性回归分析 所使用的数据集（204名不同性别的子女）中，筛选男性子女，生成新的数据集：

注：

• 身高单位均为英寸；
• MEAN为父亲、母亲身高的平均值。

试分析父母身高与成年儿子身高的相关关系。

---

对于本例，我们可以先进行散点图的绘制，观察各变量间关系的大致趋势。

1. 绘制散点图

操作：

点击Graphs -> Legacy Dialogs -> Scatter/Dot

选择Matrix Scatter，将全部变量放入Matrix Variables 列表中：

最终生成如下散点图：

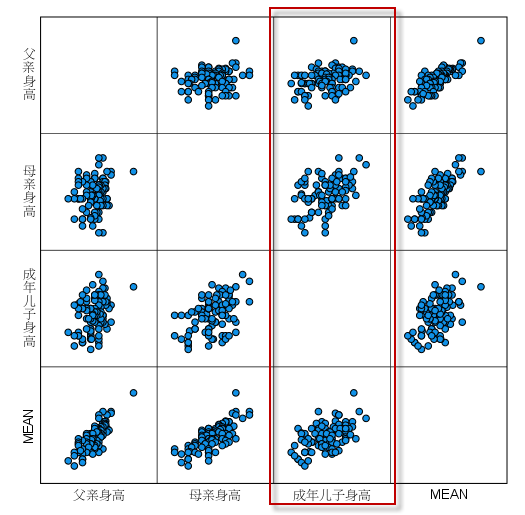
我们可以看到，父母的平均身高与成年儿子的身高之间，线性趋势相对比较明显。

2. 简单相关分析操作

选择分析【Analyze】菜单下的相关分析【Correlate】中的【Bivariate】（两变量相关），并将上述4个变量全部放入Variables列表中

相关系数的计算方法，默认已经选择了Pearson，点击【OK】即可输出Pearson相关分析的统计结果。

3. 结果解读

本例（SPSS 23 64位）输出结果如下：

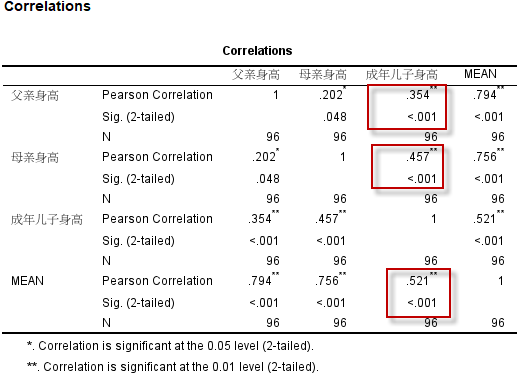
结果显示，父亲身高、母亲身高、平均身高与成年儿子的身高之间，均具有线性正相关关系（Pearson相关系数均大于0、且均具有统计学意义）；其中，父母平均身高与成年儿子身高的相关系数最大，为 $r=0.52~(P \lt .001)$，可认为父母平均身高与成年儿子身高之间具有中等程度的正相关。

对于相关强度的判断，有一个粗略的标准：

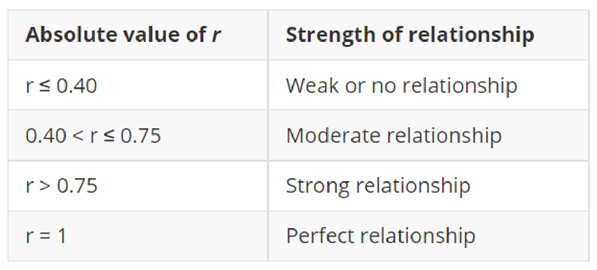
Pearson相关系数大于0.4而小于0.75（或者0.8）的，可认为相关的强度为中等。

对于Spearman相关分析，结果的解读与Pearson相关分析无异，这里不再另外举例，我们就以上述数据，看看Spearman秩相关的分析结果：

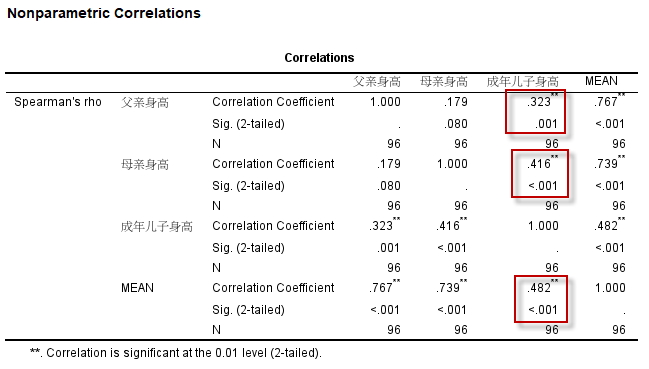
可以看到，对于同一个样本数据，两种方法得到的相关系数相差不是很大，可得到与上述Pearson相关分析相同的结论。

© By StatX..