6.4 二分类资料的Logistic回归分析
最后更新:2024-11-20
Logistic回归分析以计数资料为应变量($Y$),研究一个或多个自变量与结局$Y$之间的因果关系。
若$Y$为二分类变量(如糖尿病的发病与未发病,等等),使用数字1编码阳性结局,如发病,0编码阴性结局(对应未发病),$\pi$ 为 $y=1$的概率,则Logistic回归模型可表示为: $$ ln( \frac{\pi}{1-\pi}) = \beta_0 + \beta_1X_1 + \cdots + \beta_kX_k $$
Logistic回归模型与一般线性模型的区别,是对结局变量进行了logit变换: $$ logit(\pi) = ln( \frac{\pi}{1-\pi}) $$ 并用这个链接函数$logit(\pi)$(而不是直接使用$\pi$的对数值)与各自变量建立线性关系,因此,它是一种广义线性模型(Generalized Linear Model,GLEM)。
应用场景
一个应变量为计数资料(常用二分类,也可以是多分类),多个自变量(不限制资料类型),研究应变量$Y$与自变量之间的因果关系,从而确定自变量对应变量有无影响及影响的程度。
前提条件
- 观察值(observations)之间相互独立
- 链接函数($logit(\pi)$)与各自变量之间具有线性关系
- 各自变量之间相关性不强(即不存在严重的多重共线性问题)
另外,进行logistic回归分析,通常所需的样本量较大。
【实例】冠状动脉重度狭窄的危险因素分析
我们使用杜克大学心血管疾病数据库的一个公开数据集(ACATH,由范德堡大学生物统计学系的 Frank Harrell 慷慨提供),对冠状动脉重度狭窄(定义为至少一条重要的冠状动脉狭窄程度 $\ge 75 \% $)的危险因素,如性别、年龄、胸痛持续时间、胆固醇水平等进行分析。
剔除原数据集中存在缺失记录的观察值,最终的数据集包含2258条记录,如下图所示:
其中的变量:
- sex:性别,1示female,0示male
- age:年龄
- dur:胸痛持续时间
- choleste:胆固醇水平
- sigdz:结局变量,1表示冠状动脉严重狭窄,即冠状动脉严重狭窄,即至少一条重要的冠状动脉狭窄程度 $\ge 75% $
注意:这个数据集收集的,是因胸痛而转诊到杜克大学医学中心的患者,(样本中)冠脉重度狭窄的发生率很高,但这个发生率,不能代表一般人群的冠脉重度狭窄的发生率,因此,基于此数据集进行的分析,无论是否剔除缺失数据,结论均不能直接推论到一般人群。
1、Logistic回归分析操作
选择回归分析中的二分类Logistic回归:
将应变量填入dependent列表,将自变量全部放入Covariates列表中,并设置自变量中的分类变量,
这里只有性别是二分类变量,所以只需将sex放入Categorical Covariates列表中。
需要注意的是:在对话框的底部,有一个Reference Category的设置选项,默认是选定Last,意为:以性别中的最后一个编码值,也就是最大值(1)为参照,计算0 vs 1(也即 男 vs 女)的OR值,如果我们选择了First(必须点击Change按钮使设置生效),则以0为参照,计算1 vs 0,即女 vs 男的OR值,相同情况下,这两个OR值是倒数的关系。
设置好自变量,就可以让软件输出最终的分析结果了,如下:
2、结果的解读
(1)模型的估计结果(分析结果1)
从模型的估计与推断结果看,性别、年龄与胆固醇水平均是冠状动脉重度狭窄的影响因素,如性别(男 vs 女),$OR=8.18, P \lt 0.001$,表明胸痛患者中,男性发生冠脉重度狭窄的风险远高于女性。
注:
OR,Odds Ratio,比值比或称优势比,其计算方法,对于以下资料(四格表):
重度狭窄 无重度狭窄 男性 1219(a) 350(b) 女性 271(c) 481(d) OR定义为 $\frac{a/b}{c/d}$,如果男性与女性人群中,重度狭窄的发生率均很低(即a<<b,c<<d),那么男性与女性重度狭窄的相对风险RR(Relative Risk,定义为$\frac{a/(a+b)}{c/(c+d)}$),可近似为OR,也就是在此情况下,我们可以认为OR就是RR,OR值就是不同性别患者发生冠脉重度狭窄的相对风险。
而对于重度狭窄发生率较高的情形,OR与RR相差较多,不能做近似处理,但OR>1者则必有RR>1,OR<1者则RR<1,两者意义相同;如本例样本数据,不考虑其它因素的影响,男性中冠脉重度狭窄者为77.7%,女性患者中冠脉重度狭窄者为39.3%($\chi^2$检验显示不同性别的发生率有差异);根据上述定义,$RR_{男 \text{vs} 女}=1.98$,$OR_{男 \text{vs} 女}=5.37$,两者相差较大,但均说明男性患者中冠脉重度狭窄的发生率较女性为高,即性别是结局(冠脉重度狭窄)的一个影响因素。
对于年龄和胆固醇这两个计量资料,我们未进行等级化编码,所以其OR值(1.076,1.009)就表示年龄或胆固醇每变化(增加)1个单位,结局的变化情况:
-
年龄每增加1岁,冠脉重度狭窄的发生率就会增加一点点(OR值=1.076,RR值比1.076低但一定>1)
-
胆固醇增加1个单位,冠脉重度狭窄的发生率就会增加一点点(OR值=1.009,RR值比1.009更低但一定>1)
此时我们的结论是确定的:年龄的增长以及胆固醇水平的升高,都将导致冠脉重度狭窄的发生率升高,因此年龄与胆固醇水平是冠脉重度狭窄的影响因素。
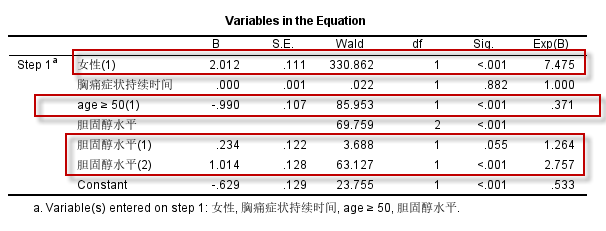
若将年龄和胆固醇水平转换为计数资料,如变换标准为:年龄以50岁为界,$\ge 50$者编码为1,$\lt 50$者编码为0;胆固醇水平以240为界,$\ge 240$者编码为1,$\lt 240$者编码为0;在Logistic回归模型中纳入性别、年龄(是否大于50岁)与胆固醇水平(是否为高胆固醇)这3个二分类资料(设置如下):
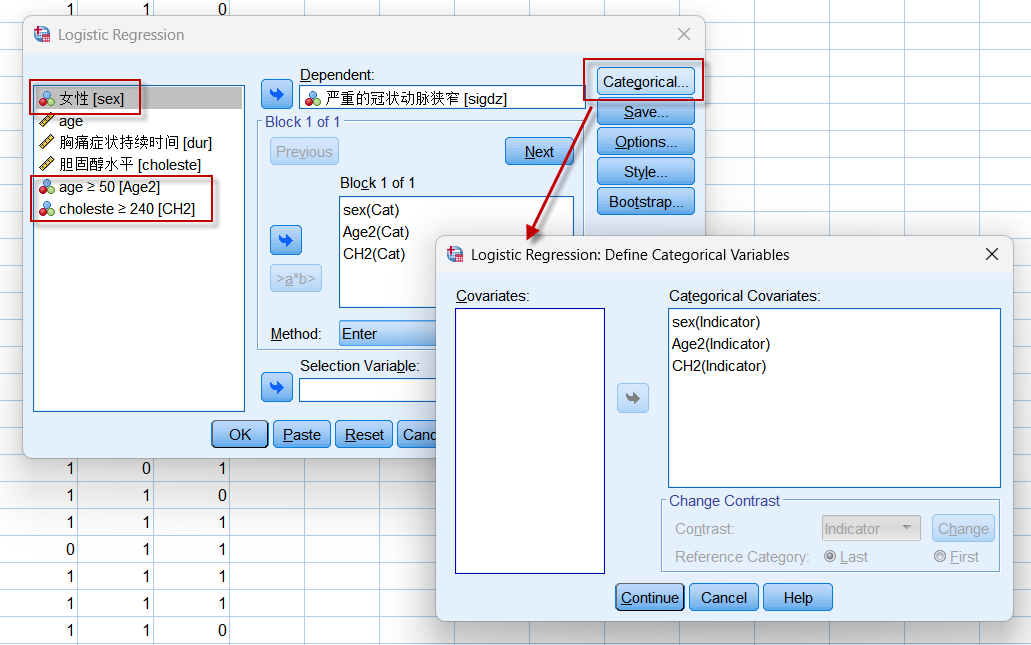
可以得到如下的回归方程:
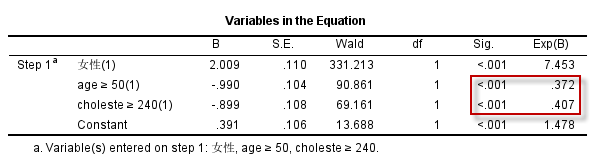
其中,年龄(是否大于50岁) 以及胆固醇水平(是否为高胆固醇)的OR值均小于1,为了与变换之前保持一致,我们可以限定OR值计算时的分子与分母:
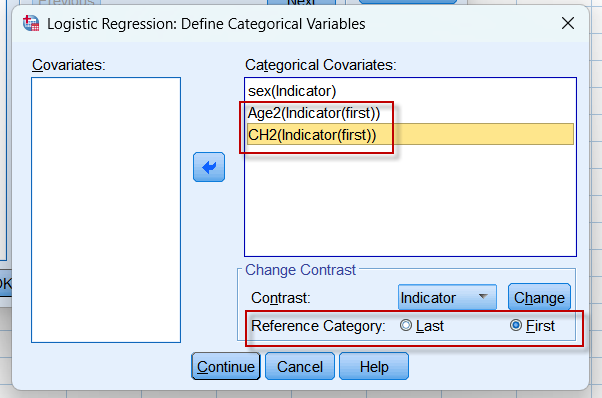
因为年龄$\ge 50$者编码为1,$\lt 50$者编码为0;胆固醇水平$\ge 240$者编码为1,$\lt 240$者编码为0,将Reference Category设定为First(需要点击上面的Change按钮使设定生效)以后,计算OR值就以编码中较小的值为参照,也就是以0所代表的分类为分母,得到的OR值就是$OR_{年龄:1 \text{vs} 0}$以及$OR_{胆固醇:1 \text{vs} 0}$ (分析结果二):
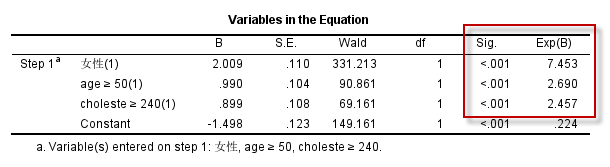
我们的推断:
- 胸痛患者中,男性冠脉重度狭窄的风险远高于女性(OR=7.45,P<0.001);
- 胸痛患者中,年龄在50岁以上(含)者,冠脉重度狭窄的风险高于50岁以下者(OR=2.69,P<0.001);
- 胸痛患者中,高胆固醇水平(定义为$\ge 240\text{mg/dL}$)者,冠脉重度狭窄的风险高于低胆固醇水平者(OR=2.46,P<0.001);
通过以上的分析,我们可以看到,在Logistic回归分析中,主要是以OR值来解释自变量对于应变量的影响,而OR的计算,对于计数资料,需要明确谁在分母位置,通过Reference Category的设置,可以设定编码中的最小值(设置为First)为参照即分母,也可以设定编码中的最大值(设置为Last)为分母,同一样本数据,不同的设置,得到的OR值互为例数;对于计量资料,OR值就是每增加1个单位风险的变化情况,比如年龄,如果不做变换,其OR值为1.076(第1个分析中),为便于理解,该OR值可以视为如下计算过程取得:
有些患者年龄为$x+1$岁,与那些年龄为$x$岁的患者相比,冠脉重度狭窄的风险是升高了还是降低了?
| 重度狭窄 | 无重度狭窄 | |
|---|---|---|
| $x+1$ | a | b |
| $x$ | c | c |
通过$OR=\frac{a/b}{c/d}$ 即可反映,而此OR与模型中年龄的OR值意义完全相同。
(2)关于模型中自变量、应变量的编码
应变量的编码:
使用SPSS进行Logistic回归分析,在输出结果中,有两个表格表示分别表示应变量和自变量中计数资料的编码:
这个表格中,Original Value是应变量的原始值,本例中采用1(冠脉重度狭窄为是)和0(冠脉重度狭窄为否)进行编码,Internal Value是SPSS软件进行Logistic回归时,对应变量进行建模的标识,在进行Logit变换时,以Internal Value=1的分类为分子: $$ logit( \pi_{y=1} ) = ln(\frac{ \pi_{y=1} }{1- \pi_{y=1}}) $$ 也就是实际的Logistic回归方程为: $$ ln(\frac{ \pi_{是} }{1- \pi_{是}}) = \beta_0 + \beta_1X_1 + \cdots + \beta_kX_k $$ 其中$\pi_{是}$ 为冠脉严重狭窄的概率。
如果将应变量的编码方式稍改一下:仍用1表示冠脉重度狭窄,而用2表示冠脉无重度狭窄,样本中的其它数据不变,则Dependent Variable Encoding表如下结果:

在SPSS进行Logistic回归分析时,logit变换仍以Internal Value=1的分类为分子,即:$logit( \pi_{y=1} ) = ln(\frac{ \pi_{y=1} }{1- \pi_{y=1}})$,而此时等于1的分类,对应的原始数据为“否”(编码为2),实际的Logistic回归方程为: $$ ln(\frac{ \pi_{否} }{1- \pi_{否}}) = \beta_0 + \beta_1X_1 + \cdots + \beta_kX_k $$ 其中$\pi_{否}$ 为冠脉不是严重狭窄的概率,结果回归方程就变成了:
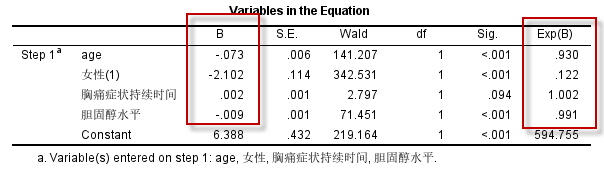
此结果与前面的分析结果1相比,回归系数互为相反数,而OR值互为倒数,在自变量(及编码)未变化的情况下,这种编码方式得到的结果,进行解释就要小心,不能因为年龄的OR值0.93小于1,就说随年龄增加,冠脉严重狭窄的风险在降低,实际上这个方程拟合的结果中:年龄每增加1岁,冠脉不是严重狭窄的概率就会降低一点点,也就是年龄增加冠脉严重狭窄的风险会上升。
为了避免出现上述拟合阴性事件的问题(导致结果的解释很别扭),我们一般使用1编码阳性事件,而用0编码阴性事件,一个原则:阳性事件的编码值要大于阴性事件的编码值,这样就可以拟合阳性事件的Logistic回归方程,便于我们解释各自变量对结局的影响。
自变量的编码
对于自变量的编码(当然只有计数资料存在编码问题),SPSS软件会自动的将设置为分类变量的自变量,编码为1个或多个哑变量(Dummy Variable),这些哑变量以括号结尾,括号中的数字表示第几个哑变量。哑变量的个数是分类数减1,如二分类资料会生成1个哑变量,而3分类资料会生成2个哑变量,等等。
比如:使用200、240这两个界值,将胆固醇水平的原始值,转换为3分类的等级资料:$\le 200 \text{mg/dL}$者编码为1,$\le 240 \text{mg/dL} 且 \gt 200 \text{mg/dL}$者编码为2,$\gt 240 \text{mg/dL}$者编码为3,并使用编码1对应的分类为参照(设置方法同前),SPSS软件就会自动生成2个哑变量,如下表:

Logistic回归分析中,所有设置为分类变量的自变量,哑变量编码结果,全部放置在Category Variable Codings(分类变量编码)表中,Parameter Coding中带有括号的列,就是哑变量的编码结果,与Logistic回归方程中结尾带有括号的分类变量一一对应,如下图(分析结果3):
以胆固醇水平为例:
Logistic回归方程中,3分类的胆固醇水平,共生成两个哑变量:
胆固醇水平(1)和胆固醇水平(2),对应的OR值分别为1.264和2.757,这两个OR值,都是以胆固醇水平等级1对应的分类(也就是胆固醇水平 $\le 200 \text{mg/dL}$者)为参照,即:
- 胆固醇水平(1):胆固醇水平等级2和等级1相比(胆固醇水平 $\le 240 \text{mg/dL} 且 \gt 200 \text{mg/dL}$者 vs 胆固醇水平 $\le 200 \text{mg/dL}$者 ),OR=1.264(P=0.055),显示冠脉重度狭窄的风险增加但无统计学意义;
- 胆固醇水平(2):胆固醇水平等级3和等级1相比(胆固醇水平 $\gt 240 \text{mg/dL}$者 vs 胆固醇水平 $\le 200 \text{mg/dL}$者 ),OR=2.757,冠脉重度狭窄的风险增加(P<0.001);
如何确定计算OR时的分母(即参照)?
根据Category Variable Codings(分类变量编码)表,看Parameter Coding(带括号的,也就是哑变量)那几列:
每个分类的自变量,有且仅有1行,Parameter Coding中的哑变量编码值全部为0,比如胆固醇水平,等级1这1行,Parameter Coding中的哑变量编码值全部为0,则等级1就是参照,就算OR值都以等级1为参照;
同理:年龄这个分类变量(二分类资料,编码为1个哑变量),Parameter Coding中的哑变量编码值为0的那一行,是年龄$\ge 50$ 者,故计算出的OR值是年龄小于50者与年龄≥50者对比;
而性别,Parameter Coding中的哑变量编码值为0的那一行对应的是女性(是),故计算的OR值,是男性与女性相比,风险的变化情况。
如何确定计算OR时的分子?
根据Parameter Coding中的哑变量编码值为1的那1行来确定:
如胆固醇水平(1)这个哑变量,我们已经确定OR的分母是胆固醇等级1,而分子,就是Parameter Coding中(1)取值1的那1行,即胆固醇等级2;胆固醇水平(2)这个哑变量,就是Parameter Coding中(2)取值1的那1行,即胆固醇等级3,其它的分类变量以此类推:
正确的认识OR值的分子与分母,才能正确地解释OR的实际含义,否则就很容易出错。
这一节内容有点偏多,先写到这。本节,我们了解了Logistic回归如何操作,如何利用OR值来解释自变量对结局的影响,而OR值的计算,受Logistic回归拟合的事件,以及自变量中分类变量如何编码的影响,故重点介绍了应变量如何编码、自变量如何编码,莫要搞错,搞错出笑话。
其他内容,如Logistic回归模型的评价、模型的诊断等,我们将放在另一节中进行介绍。
© By StatX..